Conjuntos
1)(FATEC-SP) Se A= {2, 3, 5, 6, 7, 8}, B= {1, 2, 3, 6, 8} e C={1, 4, 6, 8}, então:
a) (A-B) n C = {2}
b) (B-A) n C = {1}
c) (A-B) n C = {1}
d) (B-A) n C= {2}
e) n.d.a.
2)(OSEC-SP) Dados os conjuntos A = {a; b; c}, B= {b; c; d} e C = {a; c; d; e}, o conjunto (A-C) U (C-B) U (A n B n C) é:
a) {a; b; c; e}
b) {a; c; e}
c) A
d) {b; d; e}
e) n.d.a.
3)(CESGRANRIO-RJ) A intersecção do conjunto de todos os inteiros múltiplos de 6 com o conjunto de todos os inteiros múltiplos d e15 é o conjunto de todos os inteiros múltiplos de :
a) 3
b) 18
c) 30
d) 45
e) 90
4) (FACET-SP) Se A={0,1}; B={{1}, {0,1}} e C={0, 1, {1}, {0, 1}, {{1}{0, 1}}, então:
a) A C B
b)A n B = {0, 1}
c) A – B =Ø
d) C- {A U B} C B
e) (A ? C) ? B
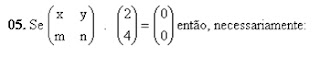
5) (UM-SP) Se A e B são dois conjuntos tais que A C B e A?Ø então:
a) sempre existe x ? A tal que x não pertence B
b)sempre existe x ? B tal que x não pertence A
c)se x ? B, então x ? A.
d)se x não pertence B, então x não pertence A
e)AnB=Ø
6) Para os conjuntos A={a} e B={a, {A}}, podemos afirmar:
a)B C A
b)A=B
c)A ? B
d)a=A
e){A} ? B
7) (PUC-SP) Se A = Ø e B {Ø } então:
a) A ? B
b) A U B = Ø
c) A = B
d) A n B = B
e) B C A
8) (FGV-SP) O número de conjuntos A que satisfazem a relação A C {1, 2, 3, 4} é:
a) 4 b)5 c)12 d) 14 e) 16
9) (FCMSCSP) Analisando as carteiras de vacinação das 84 crianças de uma creche, verificou-se que 68 receberam a vacina Sabin, 50 receberam a vacina contra sarampo e 12 não foram vacinadas. Quantas dessas crianças receberam as duas vacinas:
a) 11 b) 18 c) 22 d) 23 e) 46
10) (UFV-MG)Sabe-se que os conjuntos A e B têm, respectivamente, 64 e 16 subconjuntos. S e A U B tem 7 elementos, então A U B tem:
a) nenhum elemento b) 3 elementos c) 2 elementos d) 1 elemento e) 4 elementos
1) B 2) A 3) C 4) E 5) D
6)E 7) A 8) E 9)E 10) B
Relações e Funções
1. Os conjuntos A e B são compostos por 5 elementos cada um.
Os elementos de A formam uma PA crescente e os de B uma
PG decrescente. A PA tem o quinto termo igual a 9 e sua razão
é 3. A PG tem o primeiro termo igual a 4 e o segundo igual a 2.
Seja f: A -> B com f(an) = bn, n = 1, 2, ..., 5. Então f é uma:
A) relação mas não uma função.
B) função de IR ??IR.
C) não função pois não se pode traçar um gráfico.
D) função exponencial.
E) função bijetora.
2. Determine as funções compostas fog e gof se f(x) = x3 – 1
e g(x) = x2 + 2x.
A) fog = x6 + 6x5 + 12x4 + 8x3 – 1 e gof = x6 – 1
B) fog = x5 + 5x4 + 3x e gof = x3 – x2 – 1
C) fog = x6 – 1 e gof = x3 – 2x + 1
D) fog = x6 + 2x5 + 4x3 + 2x2 – 1 e gof = x4 – 3x3 – 2x2+ 1
E) fog = x4 + 2x3 + 2x – 1 e gof = x6 – 2x5 + 4x4 – 2x +1
03. (UNIFOR) A função f, do 1° grau, é definida por f(x) = 3x + k. O valor de k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é:
a) 1
b) 2
c) 3
d) 4
e) 5
04. (EDSON QUEIROZ - CE) O gráfico abaixo representa a função de R em R dada por f(x) = ax + b (a, b ÎR). De acordo com o gráfico conclui-se que:
a) a < 0 e b >0
b) a < 0 e b < 0
c) a > 0 e b > 0
d) a > 0 e b < 0
e) a > o e b = 0
05. (UNIFORM) O gráfico da função f, de R em R, definida por f(x) = x2 + 3x - 10, intercepta o eixo das abscissas nos pontos A e B. A distância AB é igual a:
a) 3
b) 5
c) 7
d) 8
e) 9
06. (CEFET - BA) O gráfico da função y = ax2 + bx + c tem uma só intersecção com o eixo Ox e corta o eixo Oy em (0, 1). Então, os valores de a e b obedecem à relação:
a) b2 = 4a
b) -b2 = 4a
c) b = 2a
d) a2 = -4a
e) a2 = 4b
07. (ULBRA) Assinale a equação que representa uma parábola voltada para baixo, tangente ao eixo das abscissas:
a) y = x2
b) y = x2 - 4x + 4
c) y = -x2 + 4x - 4
d) y = -x2 + 5x - 6
e) y = x - 3
08. (PUC - MG) O lucro de uma loja, pela venda diária de x peças, é dado por L(x) = 100 (10 - x) (x - 4). O lucro máximo, por dia, é obtido com a venda de:
a) 7 peças
b) 10 peças
c) 14 peças
d) 50 peças
e) 100 peças
09. (UE - FEIRA DE SANTANA) Considerando-se a função real f(x) = -2x2 + 4x + 12, o valor máximo desta função é:
a) 1
b) 3
c) 4
d) 12
e) 14
10. (ACAFE) Seja a função f(x) = -x2 - 2x + 3 de domínio [-2, 2]. O conjunto imagem é:
a) [0, 3]
b) [-5, 4]
c) ]-¥, 4]
d) [-3, 1]
e) [-5, 3]
1) E 2) A 3)E 4)A 5)D
6)a 7)c 8)a 9)e 10)b
Exponencial e logaritmo
01. (U. E. FEIRA DE SANTANA - BA) O produto das soluções da equação (43 - x)2 - x = 1 é:
a) 0
b) 1
c) 4
d) 5
e) 6
2. (PUCCAMP) Considere a sentença a2x + 3 > a8, na qual x é uma variável real e a é uma constante real positiva. Essa sentença é verdadeira se, por exemplo:
a) x = 3 e a = 1
b) x = -3 e a > 1
c) x = 3 e a < 1
d) x = -2 e a < 1
e) x = 2 e a > 1
03. As funções y = ax e y = bx com a > 0 e b > 0 e a b têm gráficos que se interceptam em:
a) nenhum ponto;
b) 2 pontos;
c) 4 pontos;
d) 1 ponto;
e) infinitos pontos.
04. (U. E. FEIRA DE SANTANA - BA) O gráfico da função real f(x) = x2 - 2:
a) intercepta o eixo dos x no ponto (1, 0);
b) intercepta o eixo dos x no ponto (0, 1);
c) intercepta o eixo dos x no ponto (2, 0);
d) intercepta o eixo dos x no ponto (0, -2);
e) não intercepta o eixo dos x.
05. (FIC / FACEM) A produção de uma indústria vem diminuindo ano a ano. Num certo ano, ela produziu mil unidades de seu principal produto. A partir daí, a produção anual passou a seguir a lei y = 1000 . (0,9)x. O número de unidades produzidas no segundo ano desse período recessivo foi de:
a) 900
b) 1000
c) 180
d) 810
e) 90
06. (U. E. LONDRINA) Supondo que exista, o logaritmo de a na base b é:
a) o número ao qual se eleva a para se obter b.
b) o número ao qual se eleva b para se obter a.
c) a potência de base b e expoente a.
d) a potência de base a e expoente b.
e) a potência de base 10 e expoente a.
07. (PUC) Assinale a propriedade válida sempre:
a) log (a . b) = log a . log b
b) log (a + b) = log a + log b
c) log m . a = m . log a
d) log am = log m . a
e) log am = m . log a
(Supor válidas as condições de existências dos logaritmos)
08. (CESGRANRIO) Se log10123 = 2,09, o valor de log101,23 é:
a) 0,0209
b) 0,09
c) 0,209
d) 1,09
e) 1,209
09. Os valores de x que satisfazem log x + log (x - 5) = log 36 são:
a) 9 e -4
b) 9 e 4
c) -4
d) 9
e) 5 e -4
10. (UERJ) Em uma calculadora científica de 12 dígitos quando se aperta a tecla log, aparece no visor o logaritmo decimal do número que estava no visor. Se a operação não for possível, aparece no visor a palavra ERRO.
Depois de digitar 42 bilhões, o número de vezes que se deve apertar a tecla log para que, no visor, apareça ERRO pela primeira vez é:
a) 2
b) 3
c) 4
d) 5
e) 6
1)E 2)D 3)D 4)A 5)D
6)B 7)E 8)B 9)D 10)D
Trigonometria
01. Na figura abaixo, r // s // t e AB ??10cm. Assim, a área do
triângulo ABC é igual a:
A) 25cm2
B) 10 2 cm2
C) 25??3 ?1?cm2
D) 25??3 ?1?cm2
E) 50??3 ?1?cm2
02. (OSEC) No triângulo ao lado, AC = 1, então:
a) AB = 2
b) AB = 3
c) AB = 4
d) AB = 5
e) AB = 6
03. (MAPOFEI) Na figura abaixo, AB = 4 cm, Â = 30º e ângulo C = 45°. Calcular BH.
04. (FEFAAP) Numa semi-circunferência de diâmetro MN e centro O, conduz-se a corda AN. Seja t a tangente à semi-circunferência no ponto A.
Responder:
a) Por que ponto passa a perpendicular à corda AN conduzida pelo ponto A?
b) Por que ponto passa a perpendicular à reta t conduzida por A?
05. (USP) Unindo-se os pontos médios dos lados de um triângulo eqüilátero cujo lado mede 3, obtém-se um novo triângulo. Unindo-se os pontos médios dos lados do novo triângulo obtém-se um terceiro triângulo.
A soma dos perímetros dos 3 triângulos obtidos é:
a) 12,50
b) 13,75
c) 15,75
d) 18
e) 21
1) D 2) A 3) 2cm 4) a – passa por M
B – passa por O 5)C
Sequência
1) Sejam uma PA e uma PG com três termos reais. A soma da PG
adicionada à soma da PA é igual a 2. Sabe-se que suas razões
são iguais ao primeiro termo da PG e que o primeiro termo da
PA é igual a 2. A razão será igual a:
A) – 1
B) 2
C) – 2
D) 1
E) 4
2) (UFPA-PA) A soma de uma PA de oito termos é 16, e a razão é -2. Então, o sexto termo é:
a) -5 b) -4 c) -3 d) -2 e) -1
3) (UFRN-RN) Se 1 + (1+a) + (1+2a) + ... + (1 + 6a) = 49, então, a é igual a:
a) 5 b) 4 c)3 d) 2 e) 1
4)(UFES-ES) Qual a razão de uma PG de três termos, onde a soma dos termos é 14 e a soma 64:
a) q=4 b) q=2 c)q=2 ou q= 0,5 d)q=4 ou q=1 e) n.d.a.
5) (UFPA-PA) Na PG de termos positivos (A, B, C), temos:
A + B + C = 91
A . C = 441
Então, A + C é igual a:
a) 21 b) 49 c)53 d) 63 e) 70
6)(PUC) Se a razão de uma P. G. é maior que 1 e o primeiro termo é negativo, a P. G. é chamada:
a) decrescente
b) crescente
c) constante
d) alternante
e) singular
7) O segundo termo de uma P. G. crescente tal que a1 = 8 e a3 = 18 é igual a:
a) 10
b) 11
c) 12
d) 14
e) 15
8) As medidas do lado, do perímetro e da área de um quadrado estão em progressão geométrica, nessa ordem. A área do quadrado será:
a) 256
b) 64
c) 16
d) 243
e) 729
9) Calcule o valor de k para que a soma dos k primeiros termos da progressão geométrica (1, 3, 9, ...) seja igual a 797161.
10) (FIA) Numa progressão geométrica, tem-se a3 = 40 e a6 = -320. A soma dos oito primeiros termos é:
a) -1700
b) -850
c) 850
d) 1700
e) 750
1) A 2) E 3) D 4) C 5) E
6)A 7)C 8)A 9)K=13 10)B
Matriz, Determinante e Sistema Lineares
01. O valor do determinante de 4a ordem, em que a23 = a32 = 2,
a22 = a33 = 3, a41 = a43 = 4 e todos os demais elementos
são iguais à unidade, é:
A) – 5
B) – 9
C) – 7
D) – 15
E) 15
02. (UNIV. CATÓLICA DE GOIÁS) Uma matriz quadrada A é dita simétrica se A = AT e é dita anti-simétrica se AT = -A, onde AT é a matriz transposta de A. Sendo A uma matriz quadrada, classifique em verdadeira ou falsa as duas afirmações:
(01) A + AT é uma matriz simétrica
(02) A - AT é uma matriz anti-simétrica
03. Se uma matriz quadrada A é tal que At = -A, ela é chamada matriz anti-simétrica. Sabe-se que M é anti-simétrica e:
Os termos a12, a13 e a23 de M, valem respectivamente:
a) -4, -2 e 4
b) 4, 2 e -4
c) 4, -2 e -4
d) 2, -4 e 2
e) 2, 2 e 4
4. (PUC) Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:
a) (A = B) . C = A . C + B . C
b) (A + B)t = At + Bt
c) (A . B)t = At . Bt
d) (A - B)C = AC - BC
e) (At)t = A
a) x = y = 0
b) x = y = m = n = 0
c) x = y e m = n
d) y = -2x e n = -2m
e) x = -2y e m = -2n
06. Na confecção de três modelos de camisas (A, B e C) são usados botões grandes (G) e pequenos (p). O número de botões por modelos é dado pela tabela:
Camisa A Camisa B Camisa C
Botões p 3 1 3
Botões G 6 5 5
O número de camisas fabricadas, de cada modelo, nos meses de maio e junho, é dado pela tabela:
Maio Junho
Camisa A 100 50
Camisa B 50 100
Camisa C 50 50
Nestas condições, obter a tabela que dá o total de botões usados em maio e junho.
07. Sobre as sentenças:
I. O produto das matrizes A3 x 2 . B2 x 1 é uma matriz 3 x 1.
II. O produto das matrizes A5 x 4 . B5 x 2 é uma matriz 4 x 2.
III. O produto das matrizes A2 x 3 . B3 x 2 é uma matriz quadrada 2 x 2
É verdade que:
a) somente I é falsa;
b) somente II é falsa;
c) somente III é falsa;
d) somente I e III são falsas;
e) I, II e III são falsas.
08. (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:
a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.
a) 3
b) 14
c) 39
d) 84
e) 258
1) B 2) (1)verdadeira
(2)verdadeira 3)B 4)C 5)E
6)
Maio Junho
Botões p 500 400
Botões G 1100 1050
7)B 8)C 9)d
Análise combinatória e Probabilidade
01. (FUVEST) Considere todas as trinta e duas seqüências, com cinco elementos cada uma, que podem ser formadas com os algarismos 0 e 1. Quantas dessas seqüências possuem pelo menos três zeros em posições consecutivas?
a) 3
b) 5
c) 8
d) 12
e) 16
02. (VUNESP) De uma urna contendo 10 bolas coloridas, sendo 4 brancas, 3 pretas, 2 vermelhas e 1 verde, retiram-se, de uma vez, 4 bolas. Quantos são os casos possíveis em que aparecem exatamente uma bola de cada cor?
a) 120
b) 72
c) 24
d) 18
e) 12
03. (MACK) Cada um dos círculos da figura ao lado deverá ser pintado com uma única cor, escolhida dentre quatro disponíveis. Sabendo-se que dois círculos consecutivos nunca serão pintados com a mesma cor, então o número de formas de se pintar os círculos é:
a) 100
b) 240
c) 729
d) 2916
e) 5040
04. (UEL) Um professor de Matemática comprou dois livros para premiar dois alunos de uma classe de 42 alunos. Como são dois livros diferentes, de quantos modos distintos pode ocorrer a premiação?
a) 861
b) 1722
c) 1764
d) 3444
e) 242
05. (UNIV. EST. DE FEIRA DE SANTANA) O número de equipes de trabalho que poderão ser formadas num grupo de dez indivíduos, devendo cada equipe ser constituída por um coordenador, um secretário e um digitador, é:
a) 240
b) 360
c) 480
d) 600
e) 720
06. (MACK) Os polígonos de k lados (k múltiplos de 3), que podemos obter com vértices nos 9 pontos da figura, são em número de:
a) 83
b) 84
c) 85
d) 168
e) 169
07. (MACK) Um juiz dispõe de 10 pessoas, das quais somente 4 são advogados, para formar um único júri com 7 jurados. O número de formas de compor o júri, com pelo menos 1 advogado, é:
a) 120
b) 108
c) 160
d) 140
e) 128
08. Do cardápio de uma festa constavam dez diferentes tipos de salgadinhos dos quais só quatro seriam servidos quentes. O garçom encarregado de arrumar a travessa e servi-la foi instruído para que a mesma contivesse sempre só 2 diferentes tipos de salgadinhos frios, e só 2 diferentes dos quentes. De quantos modos diferentes, teve o garçom a liberdade de selecionar os salgadinhos para compor a travessa, respeitando as instruções?
a) 90
b) 21
c) 240
d) 38
e) 80
09. (ITA) O número de soluções inteiras, maiores ou iguais a zero, da equação x + y + z + w = 5 é:
a) 36
b) 48
c) 52
d) 54
e) 56
10. (MACK) Dentre os anagramas distintos que podemos formar com n letras, das quais duas são iguais, 120 apresentam estas duas letras iguais juntas. O valor de n é:
a) 4
b) 5
c) 6
d) 7
c) 122
1)C 2)C 3)D 4)B 5)E
6)E 7)A 8)A 9)E 10)C
Geometria Espacial
01. (EUMT - LONDRINA) O volume de ar contido em um galpão com a forma e as dimensões dadas pela figura abaixo é:
a) 300
b) 240
c) 225
d) 210
e) 180
02. (FEI - MAUÁ) Secciona-se uma pirâmide regular de altura h por um plano paralelo à base, a uma distância x do
vértice. Pede-se x de modo que a áreas laterais da pirâmide se altura x e do tronco de pirâmide de altura h -
x sejam iguais.
03. (MAUÁ) Dado o Tetraedro de aresta L, determine, em função de L, o volume V do cone circular circunscrito,
isto é, do cone que tem vértice do Tetraedro e base circunscrita à face do Tetraedro.
04. (MAUÁ) Dado um Tetraedro regular de aresta L, determine, em função de L, a área lateral A do cilindro reto
circunscrito, isto é, do cilindro que tem uma base circunscrevendo uma face do Tetraedro e altura igual à
altura do Tetraedro.
05. (LONDRINA) O tetraedro regular ABCD tem centro O. O ângulo diedro de faces OAB e OAC mede:
a) 30°
b) 60°
c) 120°
d) 135°
e) 150°
06. (SJRP - JUNDIAI) Os vértices de um tetraedro regular de volume 1m3 são centros das faces de outro tetraedro
regular. O volume deste outro tetraedro vale:
a) 1 m3
b) 3m3
c) 9m3
d) 27m3
e) 81m3
07. (MAUÁ) Na pirâmide VABC os ângulos AVB, BVC e CVA são retos. Calcular a distância de V ao Plano
ABC sabendo-se que VA = VB = VC = 1m.
08. (OSEC) Um prisma e uma pirâmide tem bases com a mesma área. Se o volume do prisma é o dobro do volume
da pirâmide, a altura da pirâmide será:
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
09. (UnB) Sejam Pi e P2 duas pirâmides de mesma altura. A base de Pi é um quadrado e a de P2 um triângulo de
área igual a do quadrado. Então, a área lateral de Pi é:
a) sempre maior do que a de P2;
b) sempre menor do que a de P2;
c) sempre igual a de P2;
d) n.d.a.
1)B 2) 3) 4) 5)D
6)D 7) 8)C 9)D
Geometria Analítica
01. (USP) O lugar geométrico dos pontos de coordenadas (x; y) tais que y2 + (x - 1)2 = 0 é:
a) a origem
b) duas retas concorrentes
c) um ponto que não é a origem
d) conjunto vazio
e) uma reta.
02. (USP) A equação da reta perpendicular ao eixo das abscissas que passa pelo ponto médio do segmento AB, onde A(2, 3) e B é o centro da circunferência de equação x2 + y2 - 8x - 6y + 24 = 0, é:
a) y = 3
b) y = 4
c) x = 4
d) x = 3
e) 3x + 4y = 0
03. (USP) Se M é o ponto médio do segmento AB e P é o ponto médio do segmento OM, determinar a equação
da circunferência de centro P e raio OP.
04. Determinar a equação da tangente à circunferência x2 + y2 - 2x - 4y + 1 = 0 pelo ponto P(-1; 2).
05. Determinar as equações das retas (t) tangentes à circunferência x2 + y2 + 2x - 3 = 0 e que passam pelo
ponto P(5, 2).
06. (UEMT) Dada a circunferência C da equação (x - 1)2 + y2 = 1 e considerando o ponto P(2, 1), então as retas tangentes a C
passando por P:
a) Têm equações y = 1 e x = 2.
b) não existem pois P é interno a C.
c) são ambas paralelas à reta y =1
d) Têm equações y = 1 (e só uma porque P está em C).
c) Têm equações x = 1 e y = 2.
07. A equação da circunferência que passa pelo ponto (2,0) e que tem centro no ponto (2, 3) é dada por:
a) x2 + y2 - 4x - 6y + 4 = 0
b) x2 + y2 - 4x - 9y - 4 = 0
c) x2 + y2 - 2x - 3y + 4 = 0
d) 3x2 + 2y2 - 2x - 3y - 4 = 0
e) (x - 2)2 + y2 = 9
08. A equação da circunferência que passa pelo ponto A = (0; 2) e é tangente na origem a reta r y + 2x = 0, é:
a) x2 + y2 - 2x - y = 0
b) x2 + y2 + 4x - 2y = 0
c) x2 + y2 - 4x - 2y = 0
d) x2 + y2 + 4x + 2y = 0
e) x2 + y2 + 4x + 2y = 0
09. A equação da circunferência que tangencia as retas x + y = 0 e x + y = 8 e que passa pelo ponto (0; 0) é:
a) 2 . x2 + 2y2 - 4x - 4y = 0
b) x2 + y2 - 2x - 6y = 0
c) x2 + y2 - 4x - 4y = 0
d) x2 + y2 + 4x + 4y = 0
e) n.d.a.
10. A equação da reta tangente à circunferência (x - 4)2 + (y - 5)2 = 20 e que a tangencia no ponto de abscissa
2 é:
a) x - 2y - 4 = 0
b) x + 2y - 4 = 0 e x - 2y + 16 = 0
c) x + y - 2 = 0 e x - y + 16 = 0
d) x + 2y - 4 = 0 e x - 2y + 4 = 0
e) n.d.a.
1)C 2)D 3) (x - 1)2 + (y-1)2 = 2
4) x + 1 = 0
5) y - 2 = 0 e 3x - 4y - 7 = 0
6)A 7)A 8)C 9)C 10)B
Estudo da Reta
01. (FEI) As retas 2x - y = 3 e 2x + ay = 5 são perpendiculares. Então:
a) a = -1
b) a = 1
c) a = -4
d) a = 4
e) n.d.a.
02. (USP) A equação da reta que passa pelo ponto (3; 4) e é paralela à bissetriz do 2° quadrante é:
a) y = z - 1
b) x + y - 7 = 0
c) y = x + 7
d) 3x + 6y = 3
e) n.d.a.
03. Determinar o ponto B simétrico de A(-4; 3) em relação à reta x + y + 3 = 0.
04. Determinar a reta perpendicular à reta de equação x + 2y - 3 = 0 no seu ponto de abscissa igual a 5.
05. Determinar a equação da mediatriz do segmento de extremos A(-3; 1) e B(5; 7).
06. As retas (r) 2x + 7y = 3 e (s) 3x - 2y = -8 se cortam num ponto P. Achar a equação da reta perpendicular a
r pelo ponto P.
07. As retas 3x + 2y - 1 = 0 e -4x + 6y - 10 = 0 são:
a) paralelas
b) coincidentes
c) perpendiculares
d) concorrentes e não perpendiculares
e) n.d.a.
08. (USP) A equação da reta passando pela origem e paralela à reta determinada pelos pontos A(2; 3) e B(1; -4)
é:
a) y = x
b) y = 3x - 4
c) x = 7y
d) y = 7x
e) n.d.a
9. Os pontos P(x, y) tais que | x | + | y | = 4 constituem:
a) um par de retas
b) um par de semi-retas
c) o contorno de um quadrado
d) quatro retas paralelas
e) o contorno de um triângulo
1)D 2)B 3) B = (-6; 1) 4) 2x - y - 11 = 0 5) 4x + 3y - 16 = 0
6) 7x - 2y + 16 = 0 7)C 8)D 9)C
Números Complexos
01. O produto (5 + 7i) (3 - 2i) vale:
a) 1 + 11i
b) 1 + 31i
c) 29 + 11i
d) 29 - 11i
e) 29 + 31i
02. Se f(z) = z2 - z + 1, então f(1 - i) é igual a:
a) i
b) -i + 1
c) i - 1
d) i + 1
e) -i
03. (FUVEST) Sendo i a unidade imaginária (i2 = -1) pergunta-se: quantos números reais a existem para os quais (a + 1)4 é um número real?
a) 1
b) 2
c) 3
d) 4
e) infinitos
04. Sendo i a unidade imaginária o valor de i10 + i-100 é:
a) zero
b) i
c) -i
d) 1
e) -1
05. Sendo i a unidade imaginária, (1 - i )-2 é igual a:
a) 1
b) -i
c) 2i
d) -i/2
e) i/2
06. A potência (1 - i )16 equivale a:
a) 8
b) 16 - 4i
c) 16 - 16i
d) 256 - 16i
e) 256
07. Se os números complexos z1 = 2 - i e z2 = x + 1, x real e positivo, são tais que |z1 . z2|2 = 10 então x é igual a:
a) 5
b) 4
c) 3
d) 2
e) 1
08. O módulo do complexo cos a - i . sen a é:
a) -1
b) -i
c) i
d) i4
e) i5
09. Calcular as raízes quadradas do número complexo 5 - 12i.
10. Achar o conjunto-verdade, em R, da equação x8 - 17x4 + 16 = 0.
1)C 2)C 3)C 4)A 5)E
6)E 7)E 8)D 9) 3 - 2i; -3 + 2i 10) V = {1, i, -1, -i, 2, 2i, -2, -2i}
Polinômios e Equações algébricas
01. Calcular o valor numérico do polinômio P(x) = x3 - 7x2 + 3x - 4 para x = 2.
02. Determinar os valores reais de a e b para que o polinômio x3 + 6x2 + ax + b seja um cubo perfeito.
03. (UESB) Se P(x) = xn - xn-1 + xn-2 - ... + x2 - x + 1 e P(-1) = 19, então n é igual a:
a) 10
b) 12s
c) 14
d) 16
e) 18
04. (UBERL) Se P(x) é um polinômio tal que 2P(x) + x2 P(x - 1) = x3 + 2x + 2, então P(1) é igual a:
a) 0
b) -1
c) 1
d) -2
e) 2
05. As soluções da equação Q(x) = 0, em que Q(x) é o quociente do polinômio x4 - 10x3 + 24x2 + 10x - 24 por x2 - 6x + 5, são:
a) -1 e 5
b) -1 e -5
c) 1 e -5
d) 1 e 5
e) 0 e 1
06. (UESP) Se o polinômio P(x) = x3 + mx2 - 1 é divisível por x2 + x - 1, então m é igual a:
a) -3
b) -2
c) -1
d) 1
e) 2
07. (UEL) Dividindo-se o polinômio x4 + 2x3 - 2x2 - 4x - 21 por x + 3, obtêm-se:
a) x3 - 2x2 + x -12 com resto nulo;
b) x3 - 2x2 + 3 com resto 16;
c) x3 - x2 -13x + 35 e resto 84;
d) x3 - x2 - 3x + 1com resto 2;
e) x3 - x2 + x -7 e resto nulo;
08. (UEL) Se o resto da divisão do polinômio p = x4 - 4x3 - kx - 75 por (x - 5) é 10, o valor de k é:
a) -5
b) -4
c) 5
d) 6
e)
09. Sejam m e n determinados de tal modo que o polinômio x4 - 12x3 + 47x2 + mx + n seja divisível por x2 - 7x + 6. Então m + n é igual a:
a) 72
b) 0
c) -36
d) 36
e) 58
10. Para que o polinômio 2x4 - x3 + mx2 - nx + 2 seja divisível por x2 - x - 2, devemos ter:
a) m = 1 e n = 6
b) m = -6 e n = -1
c) m = 6 e n = 1
d) m = -6 e n = 1
e) m = 6 e n = -1
1) P(2) = -18 2) a = 12 e b = 8
3)E 4)E 5)A
6)E 7)E 8)E 9)C 10)D









